Clustering¶
HAC BIC¶
-
class
clustering.hac_bic.HAC_BIC(cep, table, alpha=1.0, sr=False)[source]¶ BIC Hierarchical Agglomerative Clustering (HAC) with gaussian models
The algorithm is based upon a hierarchical agglomerative clustering. The initial set of clusters is composed of one segment per cluster. Each cluster is modeled by a Gaussian with a full covariance matrix (see
gauss.GaussFull).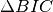 measure is employed to select the candidate clusters to group as well as
to stop the merging process. The two closest clusters
measure is employed to select the candidate clusters to group as well as
to stop the merging process. The two closest clusters 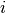 and
and
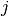 are merged at each iteration until
are merged at each iteration until 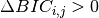 .
.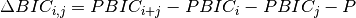
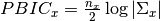
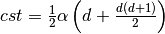
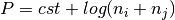
where
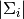 ,
, 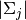 and
and  are the
determinants of gaussians associated to the clusters
are the
determinants of gaussians associated to the clusters 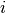 ,
, 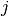 and
and 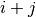 .
. 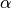 is a parameter to set up. The penalty
factor
is a parameter to set up. The penalty
factor 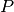 depends on
depends on 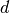 , the dimension of the features, as well as
on
, the dimension of the features, as well as
on 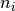 and
and 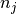 , refering to the total length of cluster
, refering to the total length of cluster
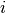 and cluster
and cluster 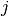 respectively.
respectively.-
_dist(mi, mj)[source]¶ Compute the BIC distance d(i,j) :param mi: a GaussFull object :param mj: a GaussFull object :return: float
-
HAC CLR¶
Tools¶
-
clustering.hac_utils.argmax(distances, nb)[source]¶ Get argmin and min indexes between 0 and nb of a distance matrix :param distances: a numpy.ndarray :param nb: int :return: row and column indexes, the value
-
clustering.hac_utils.argmin(distances, nb)[source]¶ Get argmin and min indexes between 0 and nb of a distance matrix :param distances: a numpy.ndarray :param nb: int :return: row and column indexes, the value
-
clustering.hac_utils.bic_square_root(ni, nj, alpha, dim)[source]¶ Compute a BIC square root distance described in [Stafylakis2010].
[Stafylakis2010] - Stafylakis, V. Katsouros, and G. Carayannis. The segmental bayesian information criterion and its applications to speaker diarization. Selected Topics in Signal Processing, IEEE Journal of, 4(5):857–866, 2010.
Parameters: - ni – covariance matrix of speaker i
- nj – covariance matrix of speaker j
- alpha – a threshold
- dim – the dimenssion of the features
Returns: a float
-
clustering.hac_utils.idmap_remove(idmap, index)[source]¶ ” remove data at position index :param index: the index to remove
-
clustering.hac_utils.roll(mat, j)[source]¶ delete the line j and column j in the matrix :param mat: numpy.ndarray :param j: int :return: numpy.ndarray
-
clustering.hac_utils.scores_remove(scores, index_model=None, index_seg=None)[source]¶ ” remove data at position index_model and/or index_seg :param index_model: the index in model set to remove :param index_seg: the index in segment set to remove