Segmentation¶
-
segmentation.adjust(cep, diarization)[source]¶ Moves the border of segment of diarization into lowest energy region and split segments gretter than 30s
Todo: changes numpy.convolve to the panada version
Parameters: - cep – a numpy.ndarray containing MFCC
- diarization – a Diarization object
Returns: a Diar object
-
segmentation.bic_linear(cep, diarization, alpha, sr=False)[source]¶ This segmentation over the signal fuses consecutive segments of the same speaker from the start to the end of the record. The measure employs the
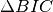 based on Bayesian Information Criterion , using full
covariance Gaussians (see
based on Bayesian Information Criterion , using full
covariance Gaussians (see gauss.GaussFull), as defined in equation below.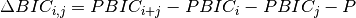
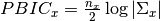
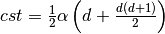
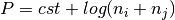
where
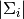 ,
, 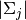 and
and  are the
determinants of gaussians associated to the left and right segmnents
are the
determinants of gaussians associated to the left and right segmnents
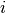 ,
, 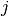 and
and 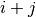 .
. 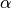 is a parameter to set up. The penalty
factor
is a parameter to set up. The penalty
factor 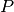 depends on
depends on 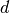 , the dimension of the cep, as
well as on
, the dimension of the cep, as
well as on 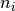 and
and 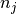 , refering to the total length of
left segment
, refering to the total length of
left segment 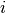 and right segment
and right segment 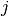 respectively.
respectively.if sr is True, BIC distance is replace by the square root bic (see
clustering.hac_utils.bic_square_root())Parameters: - cep – numpy.ndarray
- diarization – a Diarization object
- alpha – the threshold
- sr – boolean
Returns: a Diar object
-
segmentation.div_gauss(cep, show='empty', win=250, shift=0)[source]¶ Segmentation based on divergence gaussien.
The segmentation detects the instantaneous change points corresponding to segment boundaries. The proposed algorithm is based on the detection of local maxima. It detects the change points through a gaussian divergence (see equation below), computed using Gaussians with diagonal covariance matrices. The left and right gaussians are estimated over a five-second window sliding along the whole signal (2.5 seconds for each gaussian, given win =250 features). A change point, i.e. a segment boundary, is present in the middle of the window when the gaussian diverence score reaches a local maximum.
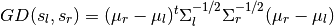
where
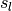 is the left segment modeled by the mean
is the left segment modeled by the mean 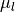 and
the diagonal covariance matrix
and
the diagonal covariance matrix 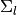 ,
, 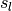 is the right
segment modeled by the mean
is the right
segment modeled by the mean 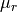 and the diagonal covariance
matrix
and the diagonal covariance
matrix 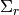 .
.Parameters: - cep – numpy array of frames
- show – speaker of the show
- win – windows size in number of frames
Returns: a diarization object (s4d annotation)